用拓扑学理解深度学习深度学习的本质
有人提了个很有意思的观点:深度学习的本质,和拓扑类似,有点像在捏橡皮泥。
乍一听一头雾水,什么拓扑啊?跟AI有什么关系?
别急,让咱们来捋一捋。
一切从一块橡皮泥开始讲起:
想象你有一坨橡皮泥,随便你怎么揉、怎么拉,只要不撕破它,这块泥的“整体形状”就还算是一样的,这种不怕揉但讲规则的几何,就是拓扑(Topology)。
而神经网络做的事,就像就是在不停地“揉橡皮泥”!
每次你训练一个神经网络,它其实在做这几步变形:
1. 先旋转一下:把数据乘一个矩阵,做个线性变化;
2. 再挪个位置:加上偏置项,整体平移一下;
3. 然后来点魔法:用tanh这种非线性函数,把橡皮泥拗成各种弯。
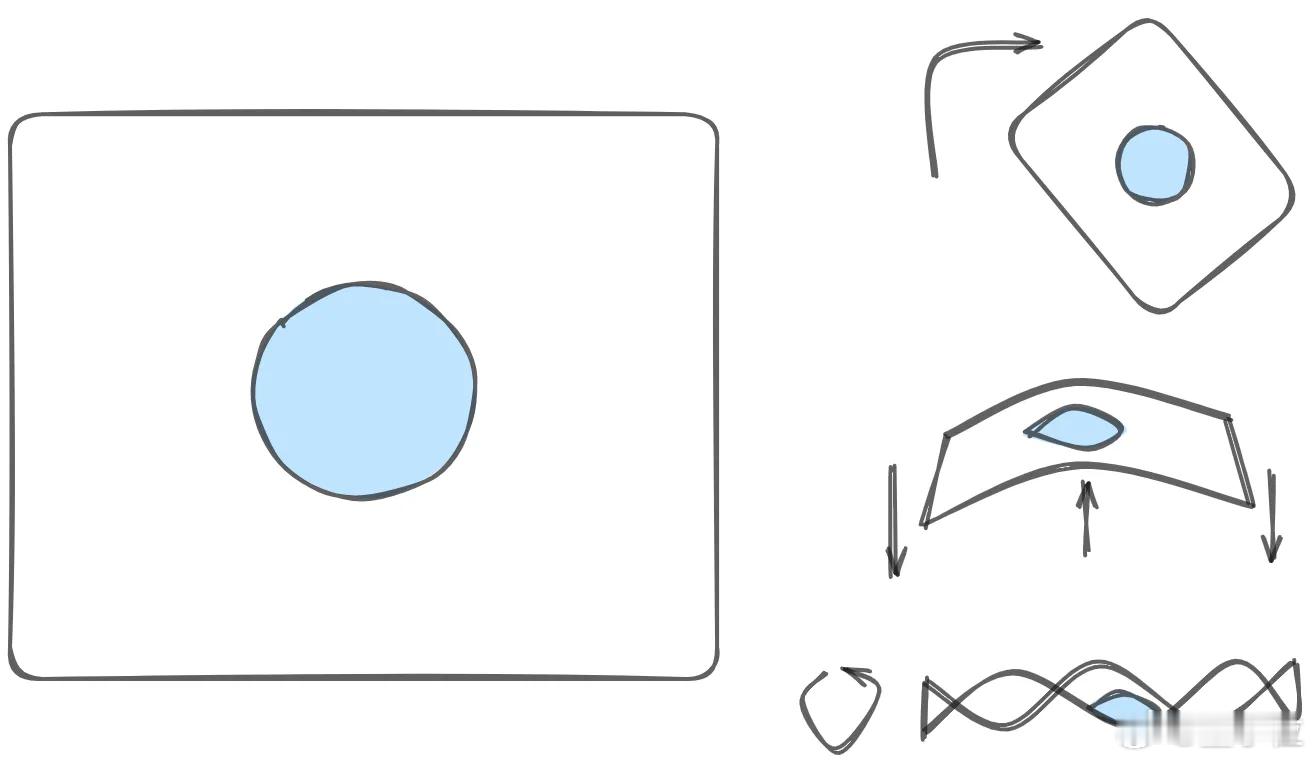
就这样反复叠加多层网络,最后这个“橡皮泥”就变成一个能把不同类别的数据分开的新形状。【图1】
那么问题来了,为什么要“揉”数据呢,不能直接分开吗?
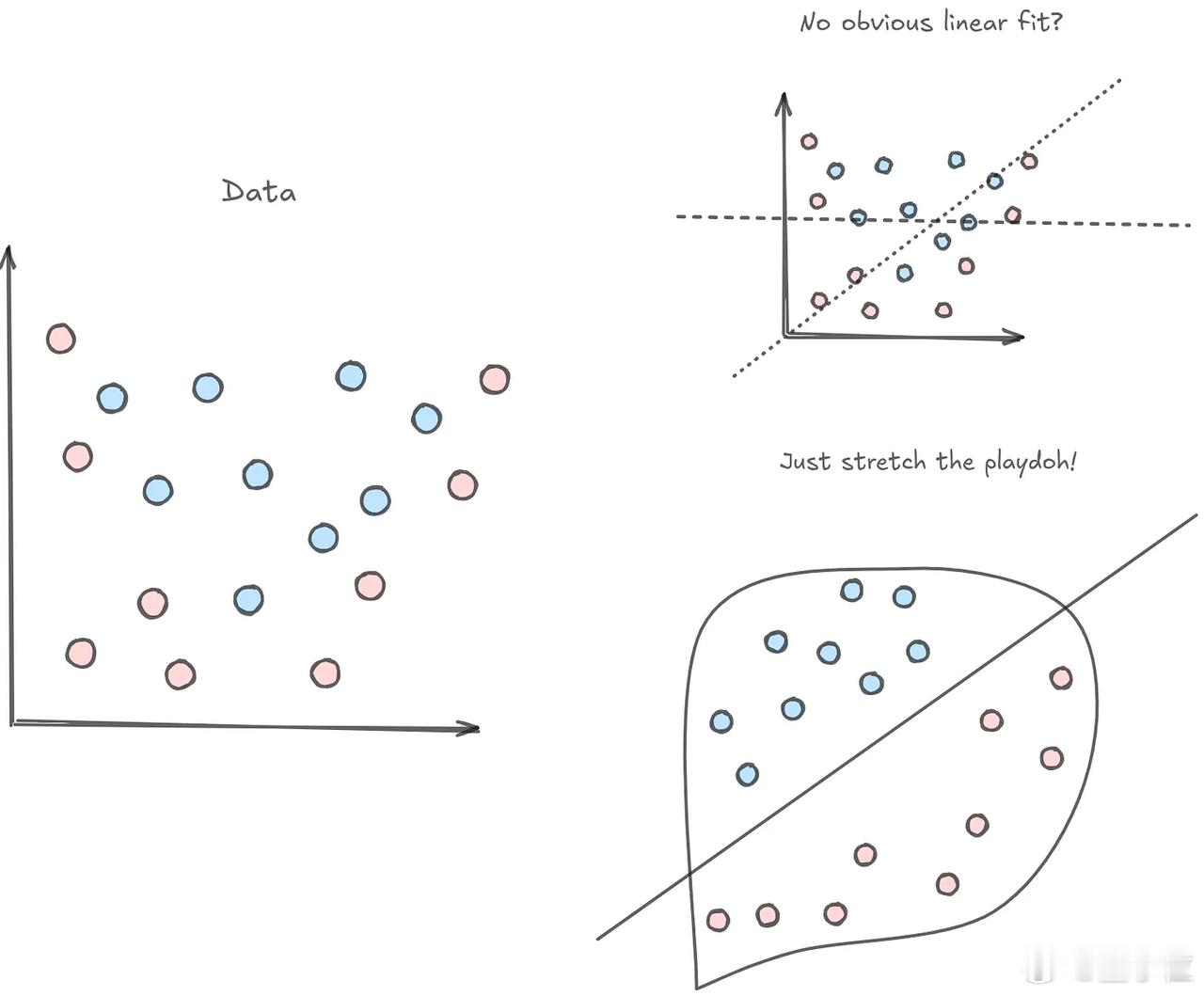
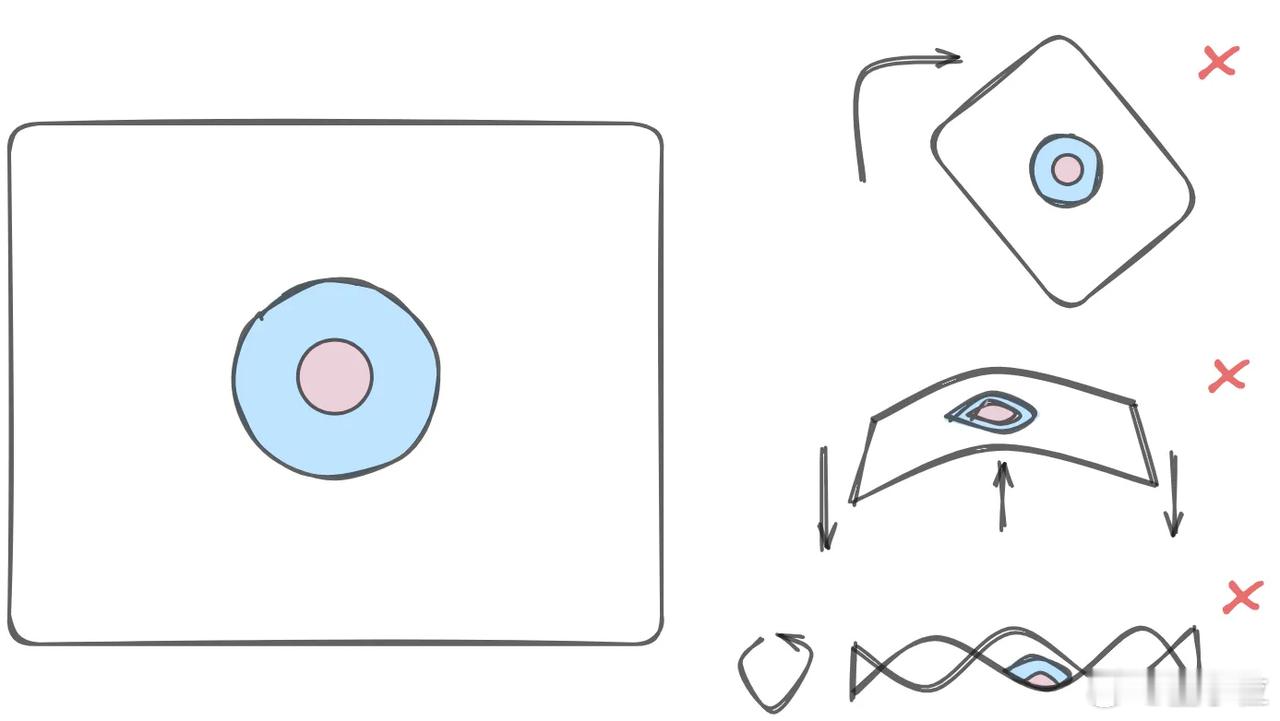
你有没有遇到过这种情况:图里有一堆红点和蓝点,肉眼一看就知道该分开,【图2】但无法用线将不同颜色的点分开,这就是维度不够的问题。【图3】
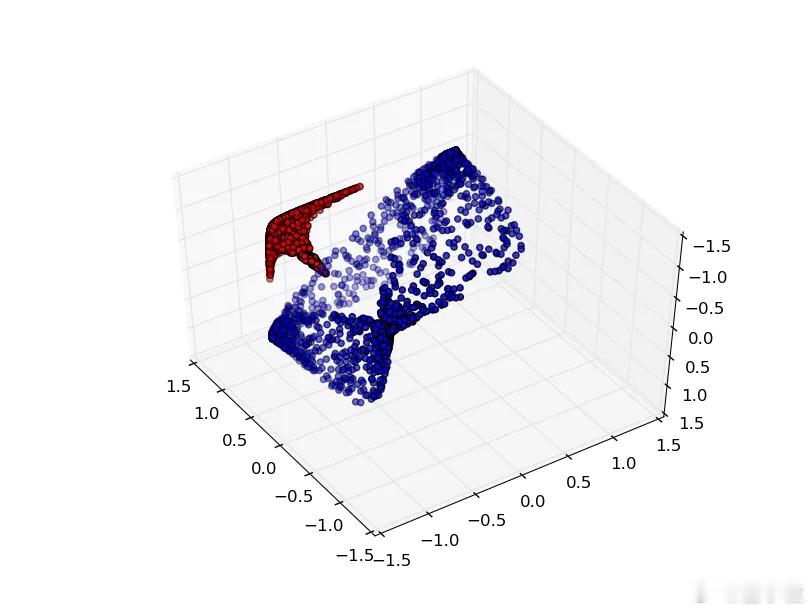
解决方法也很简单——加维度。【图4】
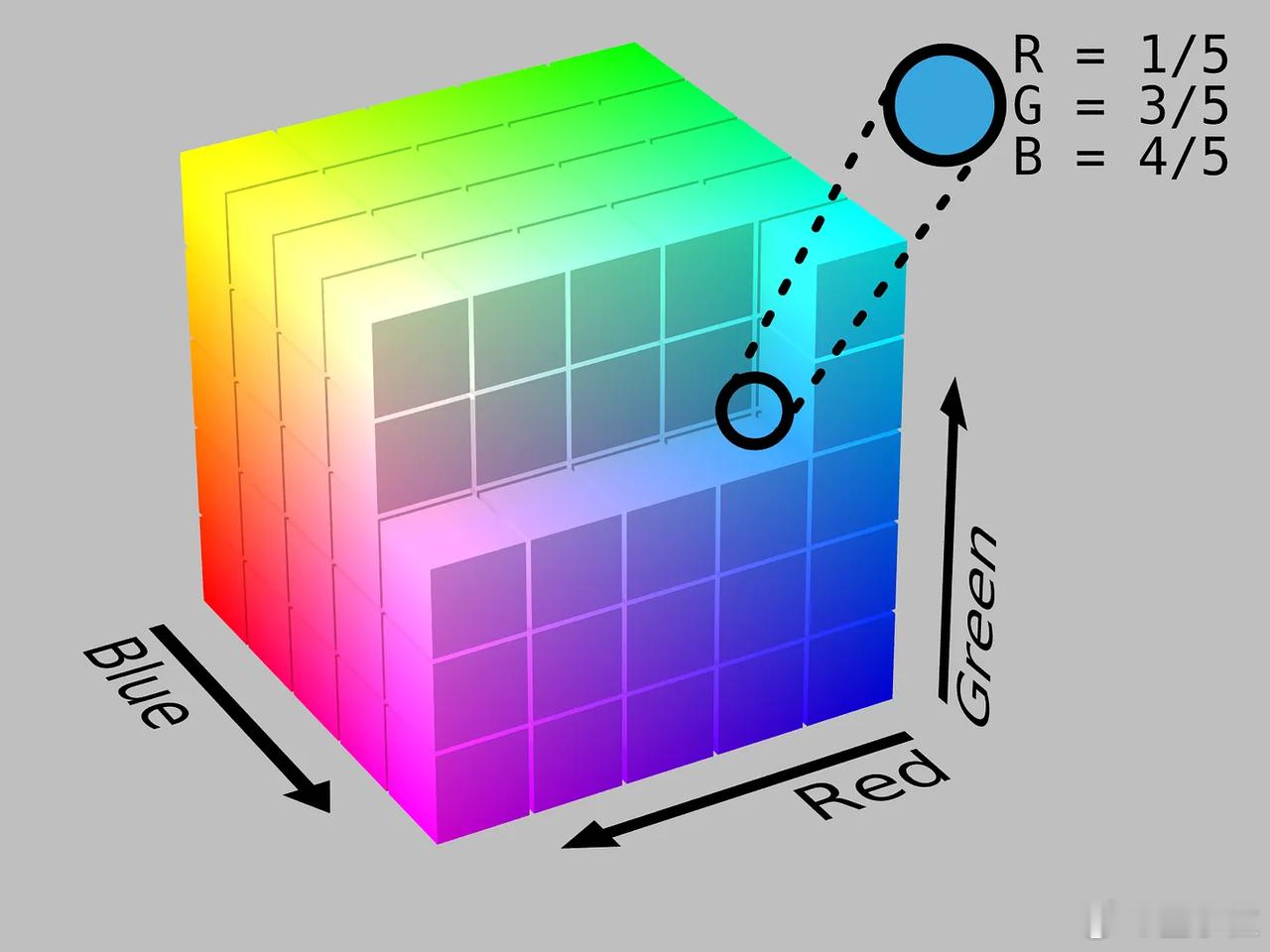
举个例子,假设你有两个分别代表红色和蓝色的RGB向量——[128, 0, 0] 和 [0, 0, 128],现在如何变成紫色呢?
你可以把它们加在一起。【图5】
从2D升到3D,就像从一张纸变成一块橡皮泥,把原来分不开的情况,变成可以一刀切开的样子。
这个过程说专业点,就是下面这几类“操作”:
- 线性变换(Linear Transformation):神经网络中的每一层都会对输入数据进行线性变换,就像把橡皮泥拉伸成不同的形状。
- 非线性激活(Non-linear Activation):接着,网络会对数据进行非线性处理,比如使用tanh函数,使得数据在高维空间中变得更加可分。
- 高维映射(High-dimensional Mapping) :如果在二维空间中无法分开数据,神经网络会将数据映射到更高的维度,在那里,数据可能就能被线性分开了。
而拓扑的奥妙在于,它可以让AI实现“一切皆可拓扑”:
- 图像:每张图片可以看作是一个高维空间中的点,神经网络通过学习,将相似的图片聚集在一起,分开猫和狗。【图6】
- 文本:词语也可以被表示为高维空间中的点。例如,“国王” - “男人” + “女人” ≈ “王后”。
- 推理过程:神经网络可以通过学习,将“好的推理”与“不好的推理”在高维空间中分开,从而提高其推理能力。
总结一下,深度学习并不陌生,本质就是在做“空间魔术”。数学家说这是拓扑,工程师说这是AI,我们可以说在捏“橡皮泥”。
感兴趣的小伙伴可以阅读原文: