[LG]《Reasoning with Latent Tokens in Diffusion Language Models》A He, S Welleck, D Fried [CMU] (2026)
为什么扩散模型在处理数独、逻辑推理这类需要全局规划的任务时,往往比传统的自回归模型表现得更出色?
本文揭示了一个关键机制:潜Token(Latent Tokens)。这不仅解释了扩散模型的优势,还为提升自回归模型的推理能力指明了新方向。
1. 扩散模型的推理密码:联合预测
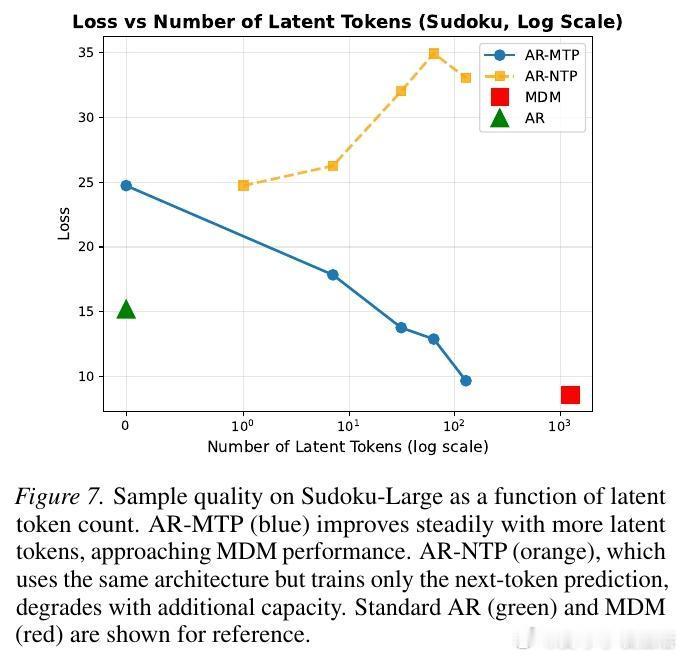
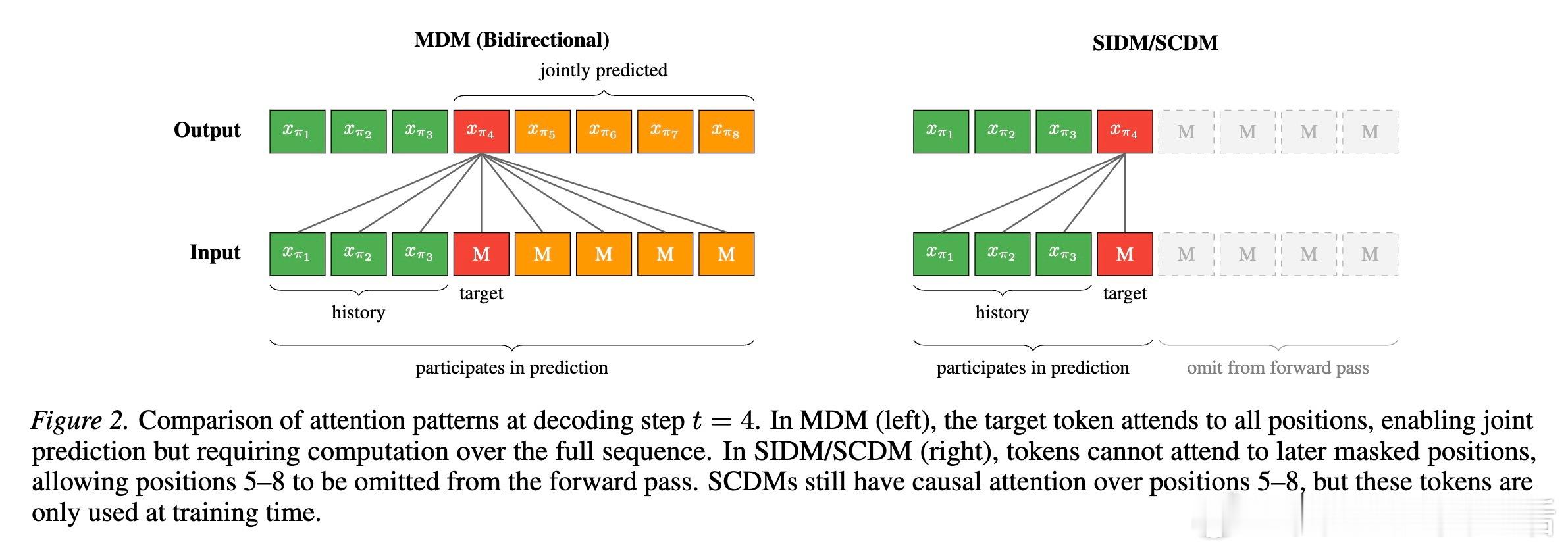
在传统的掩码扩散模型中,生成过程是从全掩码序列开始,逐步揭开代币。虽然每一步我们只选择解码一个代币,但模型在计算时实际上是在对所有未知的掩码位置进行联合预测。
研究发现,如果剥离这种联合预测机制,让模型独立预测每个位置,推理性能会大幅下降。这意味着,那些被预测但最终被丢弃的代币,并非无用的冗余,而是充当了计算的中间状态。它们就像是模型的潜意识,在正式落笔之前,已经在脑海中完成了全局的推演。
2. 什么是潜代币
我们将这些参与计算但不被解码的预测位置称为潜代币。它们本质上是模型在推理过程中利用的辅助计算空间。
在处理数独这类任务时,推断一个格子的数字往往需要同时考虑多个格子的约束。潜代币允许模型在预测目标位置时,同时捕捉其他未知位置的概率分布。这种机制与人类的思维链(Chain of Thought)异曲同工,只不过它发生在模型的潜空间里。
3. 潜代币调制:性能与速度的平衡杠杆
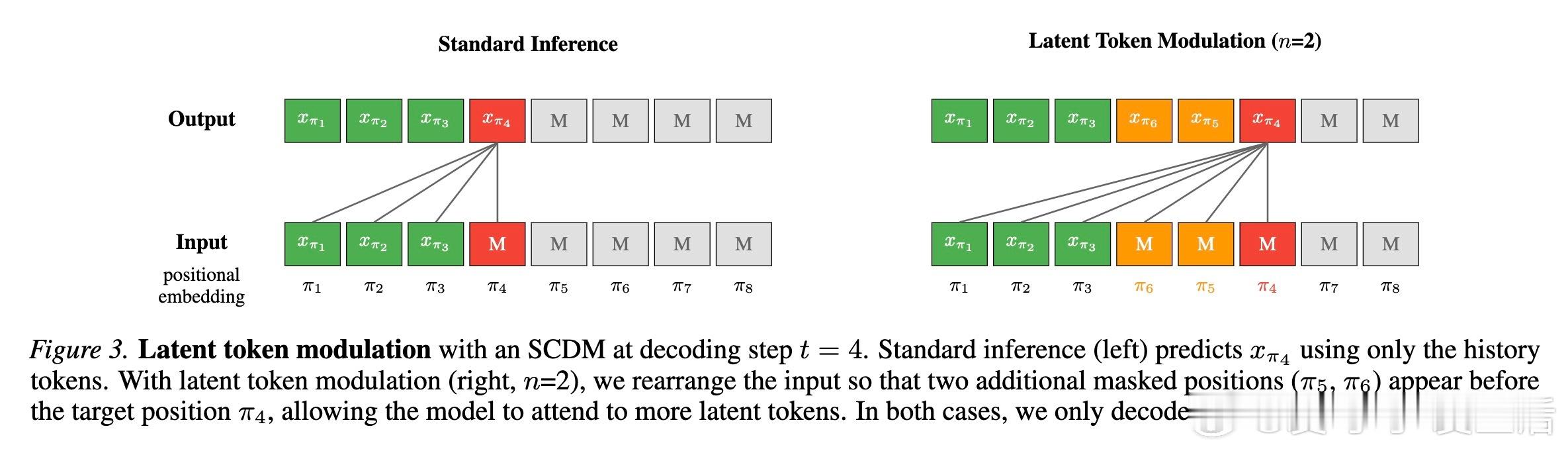
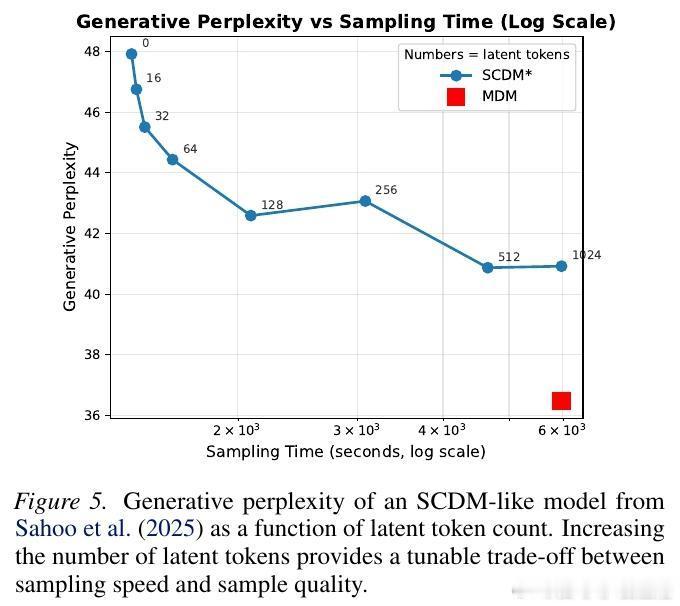
研究者提出了一种名为潜代币调制(Latent Token Modulation)的方法。通过调整推理时参与计算的潜代币数量,我们可以精确控制模型。
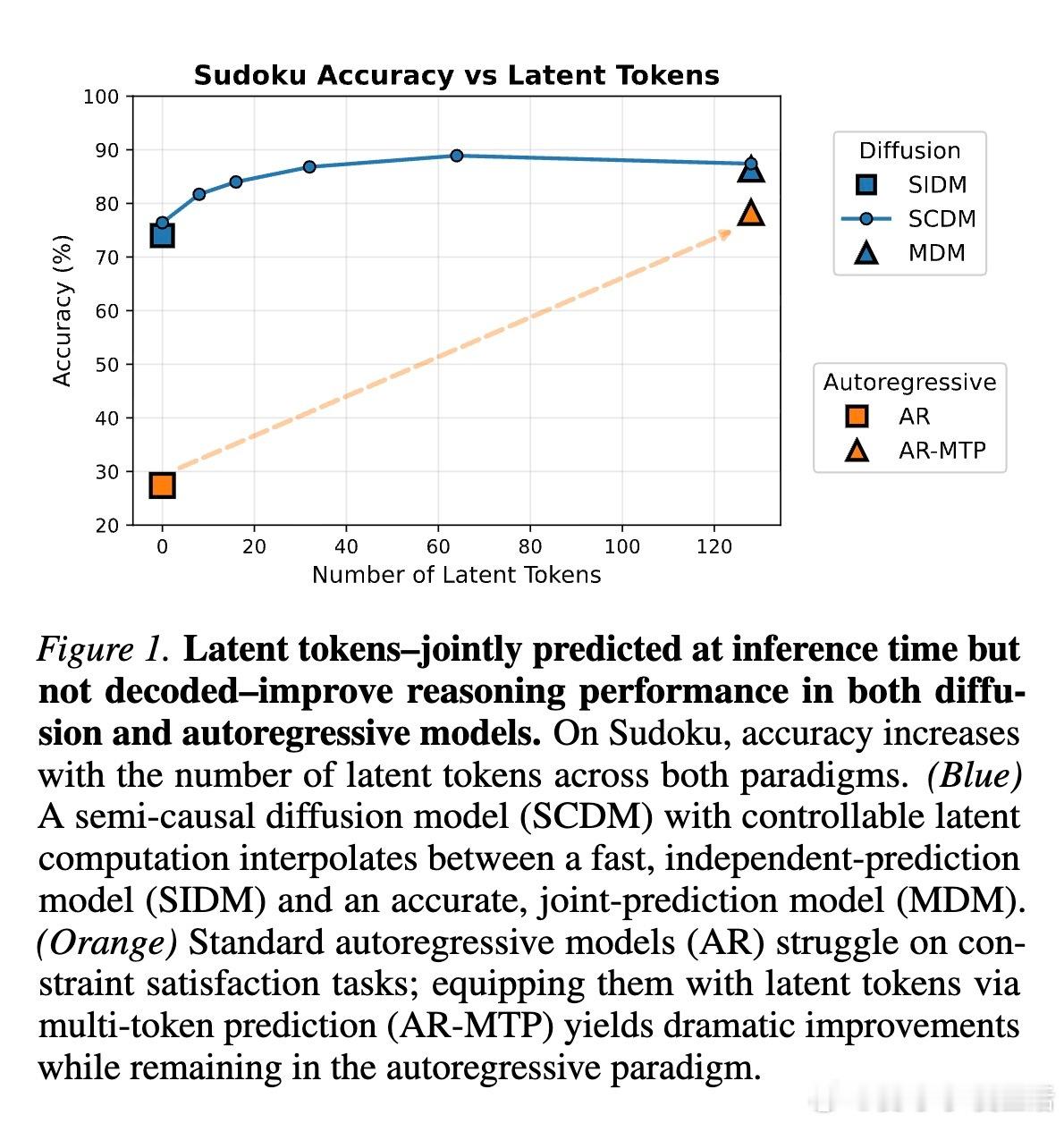
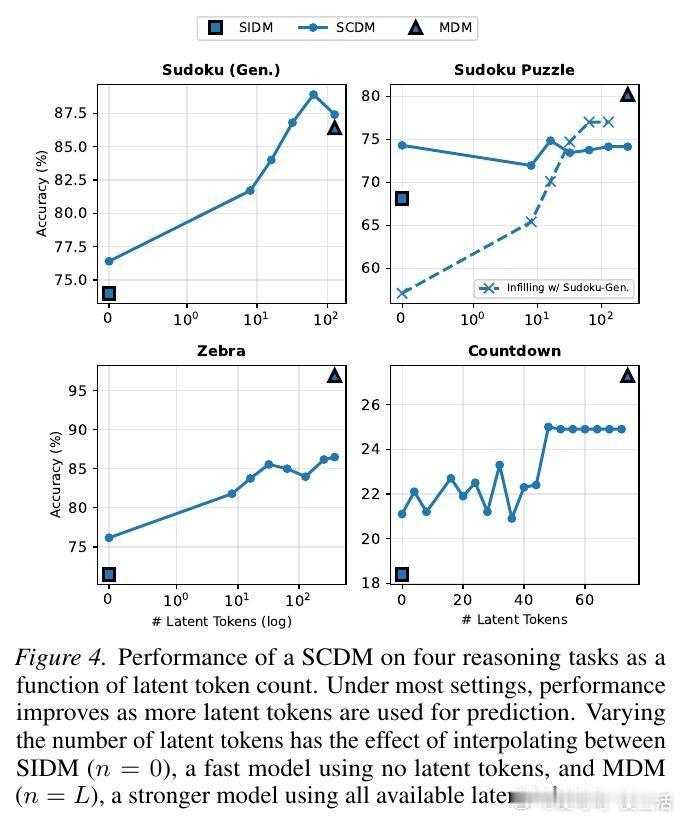
实验表明,随着潜代币数量的增加,模型在逻辑推理任务上的准确率稳步提升,在语言建模中的困惑度则持续下降。这为我们提供了一个全新的调节维度:在需要极致速度时减少潜代币,在需要深度思考时增加潜代币。
4. 赋能自回归模型:AR-MTP
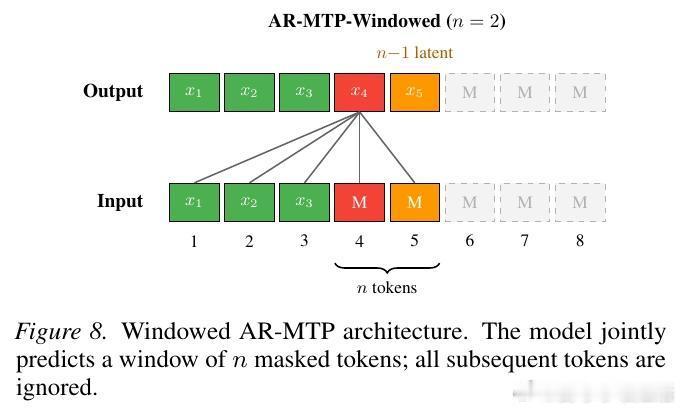
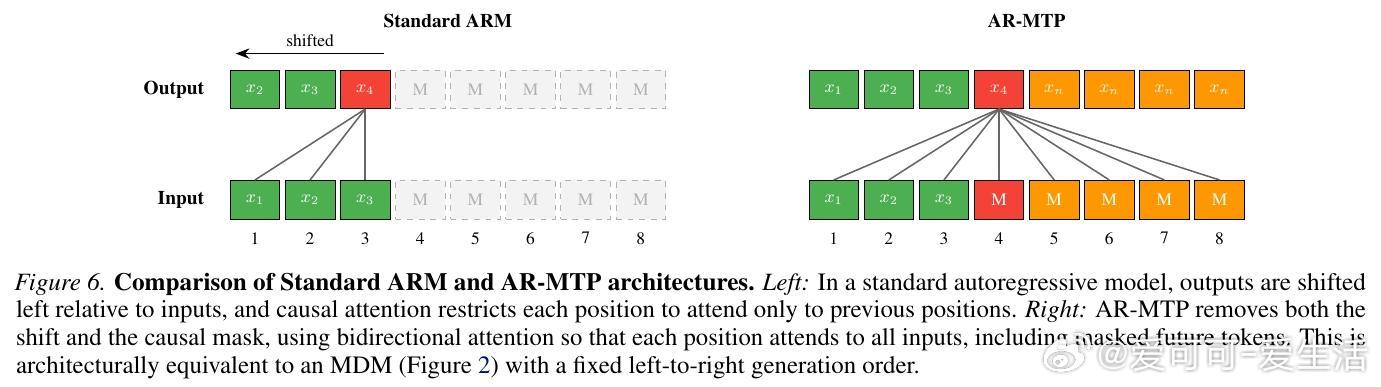
长期以来,自回归模型由于其严格的从左往右生成顺序,在处理需要全局相干性的任务时略显吃力。研究者尝试将潜代币机制引入自回归模型,开发了 AR-MTP 架构。
通过多代币预测(Multi-Token Prediction)的辅助目标进行训练,自回归模型也能在预测当前代币时利用未来的潜空间进行思考。结果令人振奋:加入潜代币后的自回归模型,在数独和逻辑谜题上的表现大幅超越了标准模型,甚至在相同计算量下优于扩散模型。
5. 深度思考与启发
这项研究告诉我们,推理的本质是全局规划与前瞻。
过去我们认为扩散模型与自回归模型是两种截然不同的范式,但潜代币的概念将它们统一了起来。性能的差异往往不在于生成的顺序,而在于模型在生成每一个词之前,动用了多少隐藏的计算资源去感知未来。
计算量即智能。潜代币不是额外的负担,而是模型通往深度推理的必经之路。当模型学会不仅看眼前的下一个词,而是同时推演未来的多种可能性时,真正的逻辑能力才开始涌现。
这种从局部预测向全局协同的转变,或许正是通往通用人工智能的关键一步。
arxiv.org/abs/2602.03769