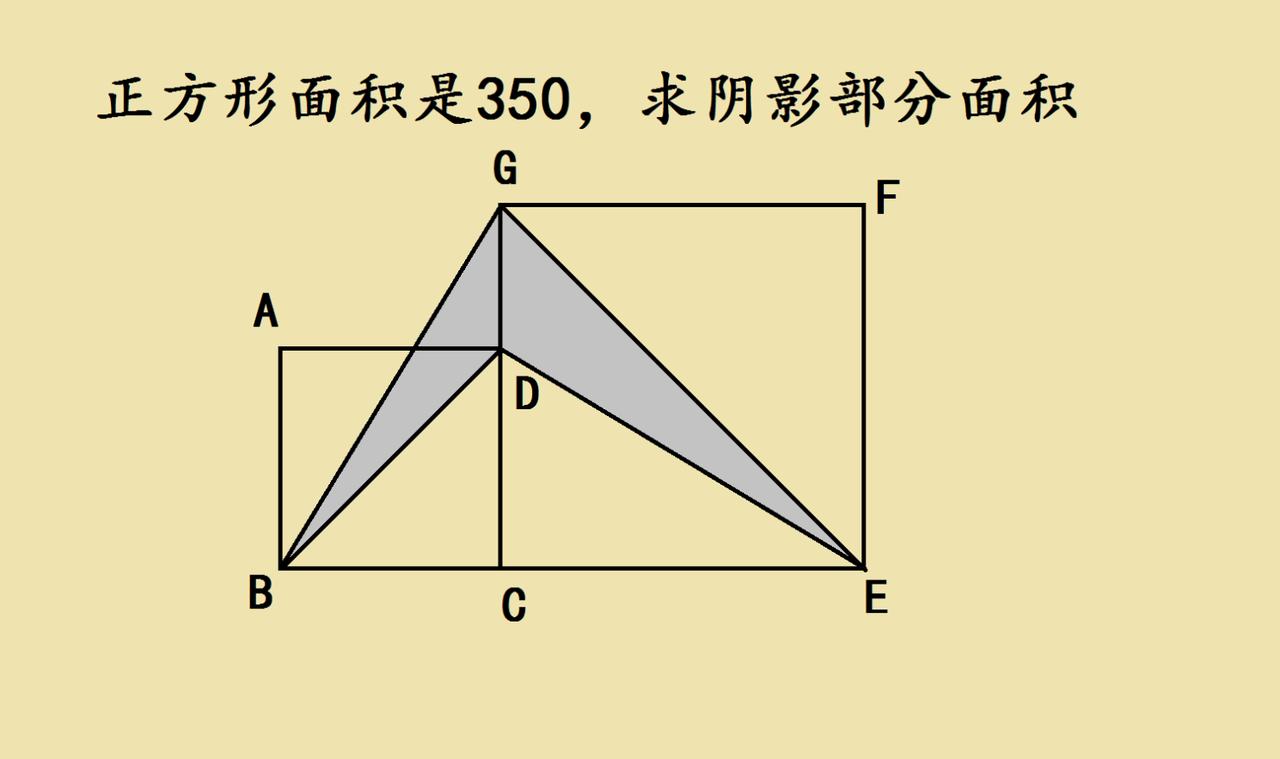
别硬算！几何题的巧解思路 拿到这道题，先别急着找边长算面积。你会发现，盯着阴影部分硬拆硬算只会钻进死胡同。换个角度，从图形关系入手才是破题关键。 先观察阴影的构成：它是由两个不规则的小三角形组成的。试着把它们和两个正方形的边长、面积差联系起来。你会发现，这两个三角形的底和高，其实刚好对应着大、小正方形的边长。 接下来是最关键的一步——等积变形。想象把其中一个三角形平移或旋转，你会发现它们可以拼成一个新的图形，而这个图形的面积，恰好和两个正方形的面积差直接相关。不需要算出任何一个正方形的边长，只需要利用“面积差是350”这个条件，就能通过图形的转化，让阴影面积和这个差值划上等号。 这类题的核心从来不是复杂计算，而是“转化”的思维：把未知的阴影，转化为已知的面积差；把分散的图形，转化为规整的关联。学会这一点，你会发现很多几何难题都变得通透了。几何巧求面积
评论列表
猜你喜欢
【8评论】【3点赞】
【6评论】【22点赞】
【2评论】【2点赞】
【31评论】【29点赞】
【18评论】【10点赞】
作者最新文章
热门分类
沉戈
老子看了半天图，觉得面积可变，然后一看文字，条件都不一样，靠，搞数学得这么不严谨吗？