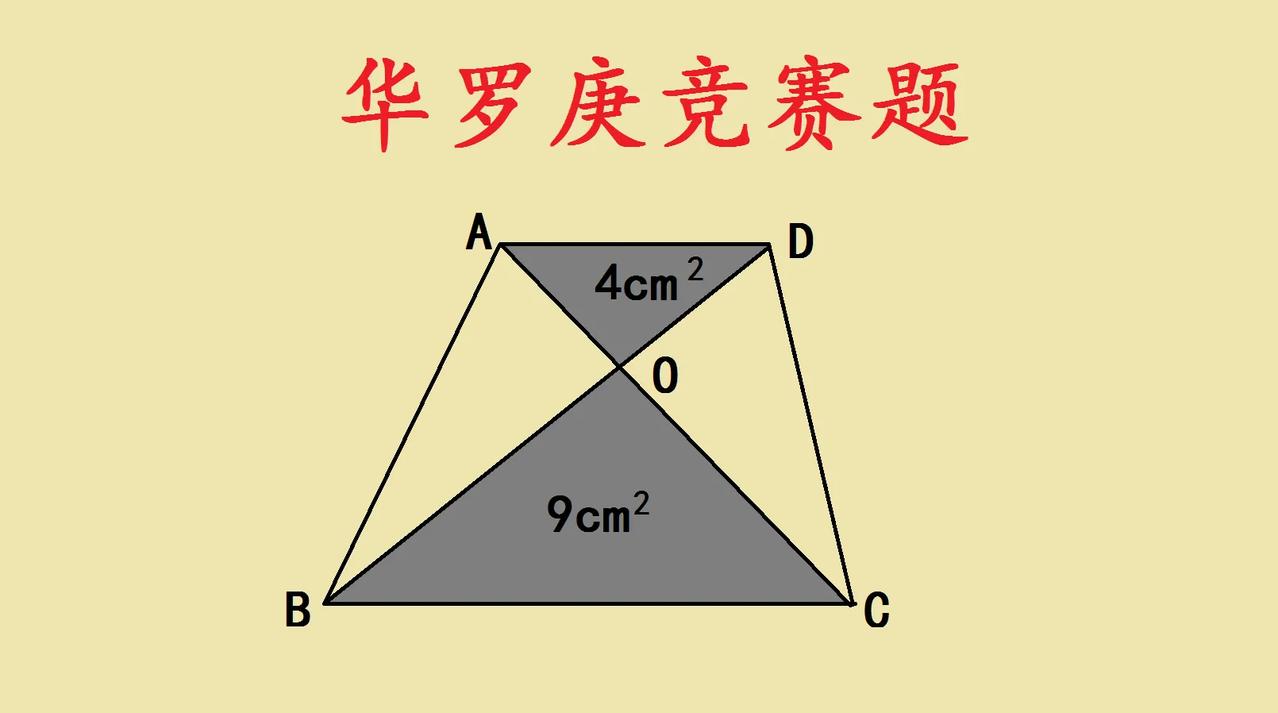
华罗庚竞赛题：揭秘梯形中的面积奥秘 家人们，今天来挑战一道华罗庚竞赛题啦！题目是关于一个梯形，梯形的对角线把它分成了四个三角形 。 其中两个三角形的面积分别是4平方厘米和9平方厘米，要求的是阴影部分面积。这题看似简单，实则暗藏玄机。 解题的核心思路在于利用三角形之间的关系。因为梯形的上下底平行，根据同底等高三角形面积相等的原理，能发现一些面积相等的三角形组合。而且，由相似三角形的性质可知，这四个三角形之间存在着特定的比例关系 。 通过这些关系，我们可以逐步推导其他三角形的面积。虽然还没算出具体结果，但解题的关键就是要敏锐捕捉这些几何图形之间的内在联系，利用三角形面积公式以及相似三角形的性质，抽丝剥茧，最终就能揭开阴影部分面积的神秘面纱。大家也来试试，看看能不能找到解题的突破口！
评论列表
猜你喜欢
【1点赞】
【1评论】【6点赞】
【6评论】【10点赞】
【4评论】【5点赞】
【122评论】【24点赞】
作者最新文章
热门分类
眼睛的主人
（9+x）/（4+x）=3/2，x=6. 那么梯形面积就是25.
kelvin
小学奥数题，蝴蝶定理。S1*S3=S2*S4 4×9=36
我是谁
题目都抄不明白就别抄了