马上一模了，几综想拿满分的同学一定要看看

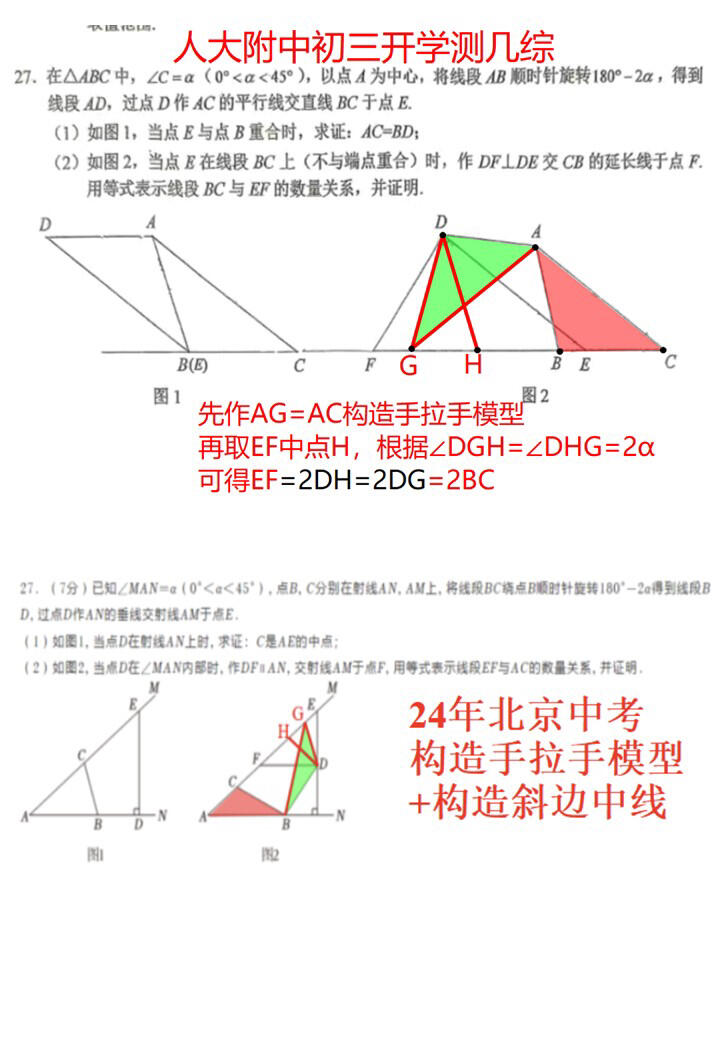
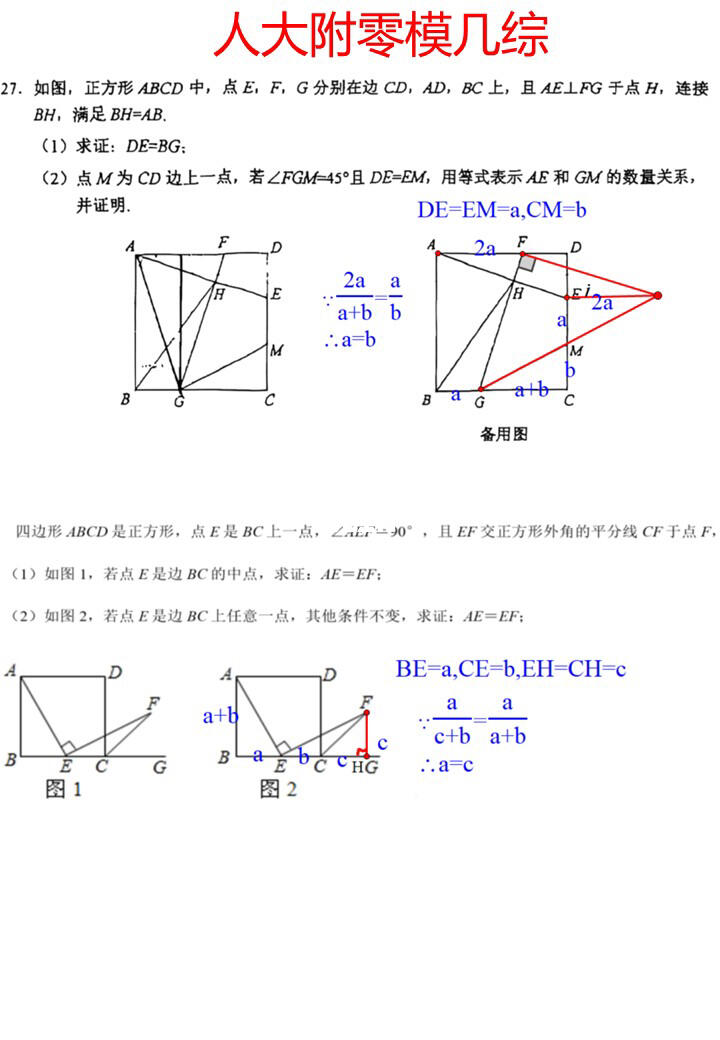
开学测几综：此题由2024年中考几何综合题改编而来，主要考查双模型构造，这也是今年几何综合题命题的热门方向，或许今年一模也会出现类似题型。因此，同学们在解答几何综合题时，若构造一个模型后仍无法解决问题，未必是思路有误，也可能需要二次构造一个小模型。这种思维模式值得积累，万一考试真遇到了呢？ 零模几综：解决的关键在于相似。首先利用45°角构造等腰直角三角形，进而得到一个平行四边形，这一步并不困难。后续想证明一个8字全等，却发现条件不足，不过8字相似是成立的，接着通过相似进行边的推导，便可推出8字全等，从而解决问题。 实际上，这种思路此前也出现过。例如后面这道经典题目，作垂线后本想证明一线三垂直全等，结果发现条件不充分，但一线三垂直相似的条件是满足的，然后通过边的推导可以推出全等，进而解决问题。 所以，这种通过相似推导边来得到全等的思路，我们需要加以积累。其实，中位线模型本质上就是一种相似导边的技巧，我们可以将其拓展到常见的8字相似、A字相似以及一线三垂直等相似模型中。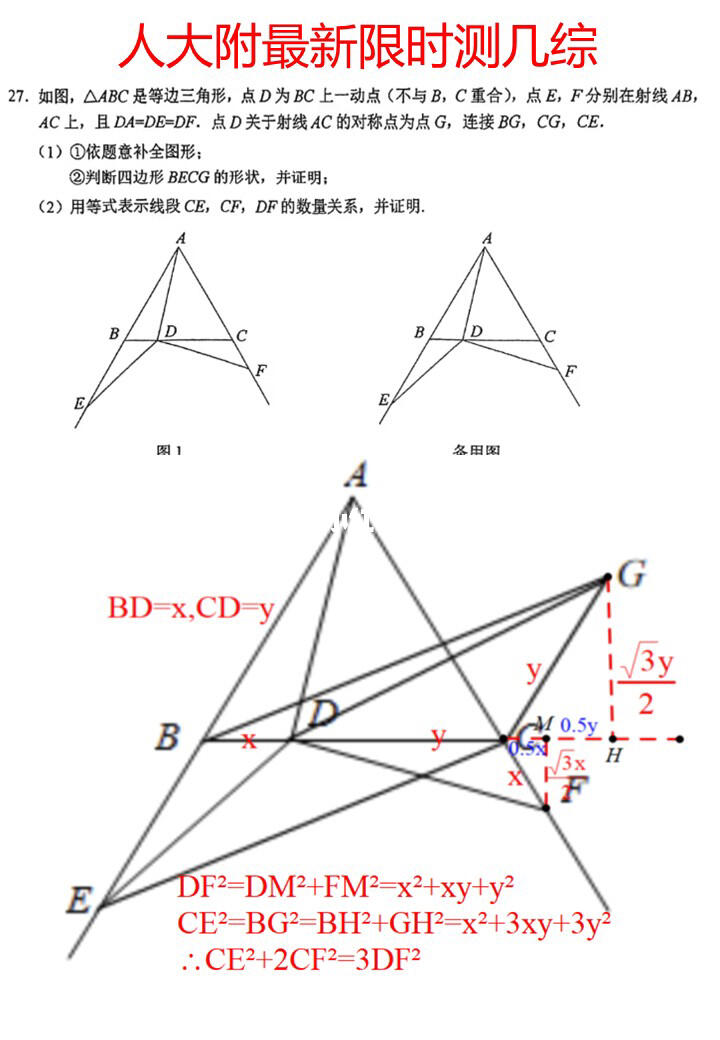 最新限时测几综：解决这道几何综合题的关键在于通过计算推导线段关系。对于线段关系问题，常规思路是通过全等将几条线段转移到一个特殊三角形中，再利用三角形的性质表示它们的关系。这种通过纯计算强行推导关系的思路并不常见，但也是解决线段关系问题的一种有效方法。也有听说部分学生通过建立坐标系来解决线段关系问题。总之，线段关系问题的基本思路是通过全等转移线段，特殊情况下也可运用计算、建系等技巧来解决。 这几道题难度较大，但有助于学生拓展思维、开阔视野，以应对更加灵活多变的几何综合题。题目之所以难，肯定是解决问题的关键技巧积累得不够或者不熟练，赶紧拿出笔记本记下来吧